달리 표준 편차 는 분산을 계산하는 동안 얻은 수치 값의 제곱근입니다. 많은 사람들이이 두 가지 수학 개념을 대조합니다. 따라서이 기사에서는 분산과 표준 편차의 중요한 차이점을 밝히려는 시도를합니다.
비교 차트
| 비교의 근거 | 변화 | 표준 편차 |
|---|---|---|
| 의미 | 분산은 산술 평균으로부터의 관측치의 가변성을 설명하는 수치입니다. | 표준 편차는 데이터 세트 내의 관측 값의 분산을 측정 한 값입니다. |
| 이게 뭐야? | 그것은 제곱의 편차의 평균입니다. | 평균 제곱근 편차입니다. |
| 다음으로 분류 : | 시그마 제곱 (σ ^ 2) | 시그마 (σ) |
| 안으로 표현됨 | 사각형 단위 | 데이터 세트의 값과 동일한 단위. |
| 나타냅니다 | 그룹의 개인이 얼마나 멀리 퍼져 있습니다. | 데이터 세트의 관측치가 평균과 얼마나 다른가? |
분산의 정의
통계에서 분산은 그룹의 구성원이 얼마나 멀리 퍼져 있는지 나타내는 변동성의 척도로 정의됩니다. 각 관찰이 평균과 다른 정도의 평균을 알아 낸다. 데이터 세트의 분산이 작 으면 평균에 대한 데이터 포인트의 근접성을 나타내지 만 분산의 값이 클수록 관측치가 산술 평균 및 서로간에 분산되어 있음을 나타냅니다.
분류되지 않은 데이터의 경우 :
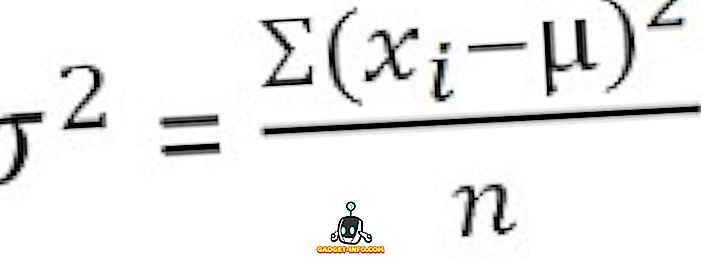
그룹화 된 빈도 분포의 경우 :
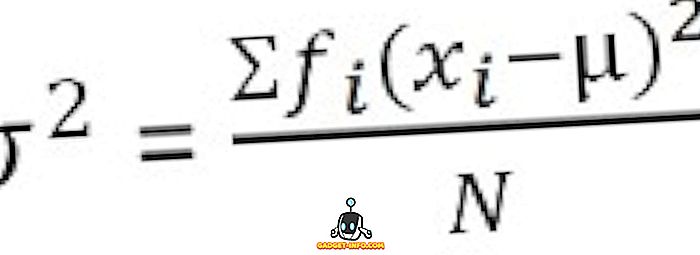
표준 편차의 정의
표준 편차는 데이터 집합에서 관측 값의 분산 양을 정량화하는 척도입니다. 낮은 표준 편차는 산술 평균에 대한 점수의 근접성을 나타내는 지표이며 높은 표준 편차가 나타납니다. 점수는 더 높은 범위의 값으로 분산됩니다.
분류되지 않은 데이터의 경우 :

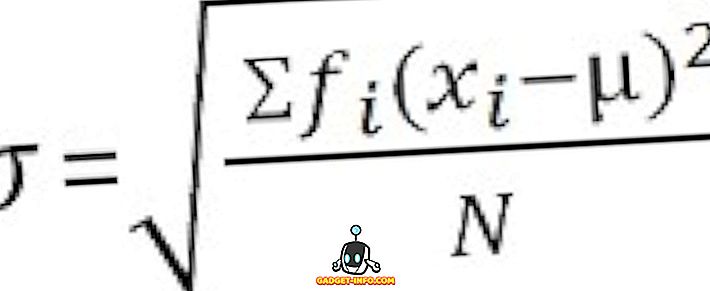
차이와 표준 편차의 주요 차이점
표준 편차와 분산의 차이는 다음과 같은 이유로 명확하게 나타낼 수 있습니다.
- 분산은 산술 평균으로부터의 관측치의 가변성을 설명하는 수치입니다. 표준 편차는 데이터 세트 내의 관측 값의 분산을 측정 한 값입니다.
- 분산은 편차의 제곱 평균입니다. 반면, 표준 편차는 제곱 평균 제곱근 편차입니다.
- 표준 편차는 시그마 (σ)로 표시되는 반면 편차는 시그마 제곱 (σ2)으로 표시됩니다.
- 분산은 일반적으로 주어진 데이터 세트의 값보다 큰 제곱 단위로 표시됩니다. 표준 편차와는 대조적으로 데이터 집합의 값과 같은 단위로 표현됩니다.
- 분산은 그룹 내의 개인이 얼마나 멀리 퍼져 나가는 지 측정합니다. 반대로 표준 편차는 데이터 집합의 관측치가 평균과 얼마나 다른지 측정합니다.
삽화
5 명의 과목에서 학생이 채점 한 점수는 각각 60, 75, 46, 58 및 80입니다. 표준 편차와 분산을 찾아야합니다.
우선, 당신은 평균을 찾아야 만합니다.

따라서 평균 (평균) 점수는 63.8
이제 분산을 계산하십시오.
| 엑스 | 에이 | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
어디, X = 관측
A = 산술 평균
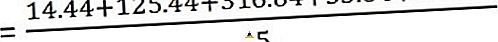
표준 편차는 -

유사점
- 분산과 표준 편차는 항상 양의 값입니다.
- 데이터 세트의 모든 관측치가 동일하다면 표준 편차와 분산은 0이됩니다.
결론
이 두 가지는 서로 다른 분야에서 중요한 역할을하는 기본적인 통계 용어입니다. 분산은 주어진 데이터 세트보다 큰 단위로 표시되는 반면, 표준 편차는 측정 값과 동일한 단위로 표현되므로 평균보다 선호됩니다.