중심 경향에 대한 이상적인 척도는 명확하게 정의되고, 쉽게 이해되며, 간단히 계산할 수있는 것이다. 그것은 모든 관측에 기초해야하며 데이터 세트에있는 극단적 인 관측에 의해 영향을받지 않아야합니다.
사람들은 종종이 두 가지 조치를 대조하지만 실제로는 서로 다릅니다. 이 기사에서는 평균과 중간의 기본 차이점을 구체적으로 설명합니다. 보세요.
비교 차트
| 비교의 근거 | 평균 | 중앙값 |
|---|---|---|
| 의미 | 평균은 주어진 값 또는 수량 세트의 단순 평균을 나타냅니다. | 중앙값은 정렬 된 값 목록의 가운데 숫자로 정의됩니다. |
| 이게 뭐야? | 산술 평균입니다. | 그것은 위치 평균입니다. |
| 대표하다 | 데이터 집합의 중심 | 데이터 집합의 중심 데이터 집합의 중간 지점 |
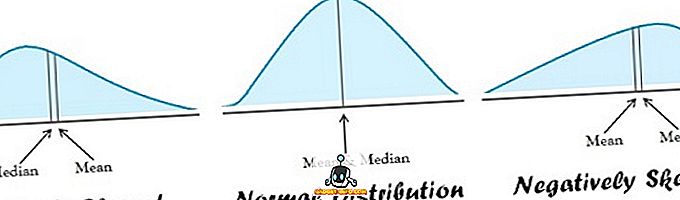
| 적용 분야 | 정규 분포 | 비뚤어진 분포 |
| 특이 치 | 평균은 특이 치에 민감합니다. | 중간 값은 특이 치에 민감하지 않습니다. |
| 계산 | 평균은 모든 관측치를 더한 다음 관측치 수로 얻은 값을 나눔으로써 계산됩니다. | 중앙값을 계산하려면 데이터 세트가 오름차순 또는 내림차순으로 정렬 된 다음 새 데이터 세트의 정확한 중간에 속하는 값이 중앙값입니다. |
평균의 정의
평균은 값 집합의 평균으로 정의되는 중심 경향의 널리 사용되는 척도입니다. 주어진 값 범위의 모델과 가장 일반적인 값을 나타냅니다. 이산 및 연속 시리즈 모두에서 계산할 수 있습니다.
평균은 모든 관측치의 합계를 데이터 세트의 관측치 수로 나눈 값과 같습니다. 변수가 취한 값이 같으면 그 평균도 같습니다. 평균은 표본 평균 (x̅)과 모집단 평균 (μ)의 두 가지 유형이 될 수 있습니다. 주어진 공식으로 계산 될 수 있습니다 :
- 산술 평균 :

n = 값의 수 - 이산 계열 :

- Continuous Servies의 경우 :

A = 가정 된 평균
C = 공통 제수
중앙값의 정의
중앙값은 중앙 경향의 또 다른 중요한 척도이며, 값을 두 개의 동일한 부분으로 나누는 데 사용됩니다. 즉, 하반부의 표본, 모집단 또는 확률 분포의 큰 부분입니다. 가장 중간 값이며 관측치가 오름차순 또는 내림차순으로 특정 순서로 정렬 될 때 얻어집니다.
중앙값의 계산을 위해서는 먼저 관측치를 가장 낮은 곳부터 가장 높은 곳 또는 가장 높은 곳에서 가장 낮은 곳으로 정렬 한 다음 아래에 주어진 조건에 따라 적합한 수식을 적용하십시오.
- 관측 수가 홀수 일 경우 :

- 관측 수가 균일하면 :

- 연속 시리즈 :

c = 선행 중간 등급의 누적 빈도
f = 중앙값 클래스의 빈도
h = 클래스 너비
평균과 중간의 주요 차이점
평균값과 중간 값의 중요한 차이점은 아래에있는 기사에서 제공됩니다.
- 통계에서 평균은 주어진 값 또는 수량 세트의 단순 평균으로 정의됩니다. 중간 값은 정렬 된 값 목록의 가운데 숫자라고합니다.
- mean은 산술 평균이고, median은 위치 평균이며, 본질적으로 데이터 세트의 위치는 중앙값의 값을 결정합니다.
- Mean은 데이터 세트의 중심을 설명하고 중간 값은 데이터 세트의 가장 중간 값을 강조 표시합니다.
- 평균은 정상적으로 분산 된 데이터에 적합합니다. 반면 데이터 분포가 왜곡 될 때 중앙값이 가장 좋습니다.
- 평균값은 중앙값의 경우가 아닌 극단 값의 영향을 많이받습니다.
- 평균은 모든 관측치를 더하고 관측치 수로 얻은 값을 나눔으로써 계산됩니다. 결과는 평균입니다. 중앙값과 반대로 데이터 세트는 오름차순 또는 내림차순으로 정렬되며 새 데이터 세트의 정확한 중간에 속하는 값은 중앙값입니다.
예
주어진 데이터 세트의 평균 및 중간 값을 찾습니다.
58, 26, 65, 34, 78, 44, 96
솔루션 : 평균을 계산하려면 관측치의 합계를 관측치 수로 나누어야합니다.

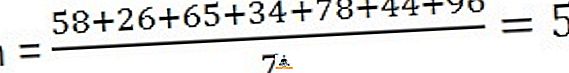
중앙값을 계산하려면 먼저 계열을 순서대로 배열하십시오 (예 : 가장 낮은 것에서 가장 높은 것)
26, 34, 44, 58, 65, 78, 96
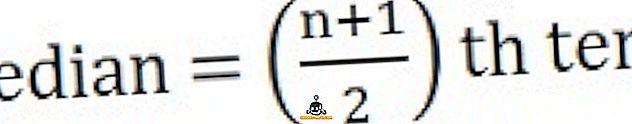
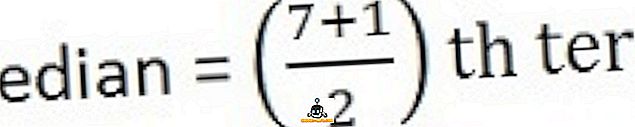
결론
위의 점을 검토 한 결과, 이 두 수학 개념이 다르다고 말할 수 있습니다. 산술 평균 또는 평균은 이상적인 측정 값의 모든 특성을 포함하고 있기 때문에 중심 경향의 가장 좋은 측정 값으로 간주되지만 샘플링 변동이 평균에 영향을주는 단점이 있습니다.
같은 방법으로, 중앙값도 명확하게 정의되고 이해하기 쉽고 계산하기 쉽고, 이 측정법의 가장 좋은 점은 샘플링 변동에 영향을받지 않는다는 것입니다. 그러나 중앙값의 유일한 단점은 모든 것을 기반으로하지 않는다는 것입니다 관찰. 개방형 분류의 경우 평균보다 중간 값이 일반적으로 선호됩니다.