상관과 회귀의 차이는 인터뷰에서 자주 묻는 질문 중 하나입니다. 더욱이 많은 사람들이이 두 가지를 이해하는 데 애매 모호합니다. 따라서이 두 가지에 대해 명확하게 이해하려면이 기사를 자세히 읽으십시오.
비교 차트
| 비교의 근거 | 상관 관계 | 회귀 분석 |
|---|---|---|
| 의미 | 상관 관계는 두 변수의 상호 관계 또는 연관성을 결정하는 통계적 척도입니다. | 회귀 분석은 독립 변수가 종속 변수와 어떻게 수치 적으로 관련되는지를 설명합니다. |
| 용법 | 두 변수 간의 선형 관계를 나타냅니다. | 최선의 라인을 맞추고 다른 변수에 기초하여 하나의 변수를 추정하십시오. |
| 종속 변수 및 독립 변수 | 차이 없음 | 두 변수가 다릅니다. |
| 나타냅니다 | 상관 계수는 두 변수가 함께 움직이는 정도를 나타냅니다. | 회귀 분석은 알려진 변수 (x)의 단위 변경이 추정 변수 (y)에 미치는 영향을 나타냅니다. |
| 목표 | 변수 사이의 관계를 표현하는 수치를 찾으려면. | 고정 변수의 값에 기초하여 무작위 변수의 값을 추정합니다. |
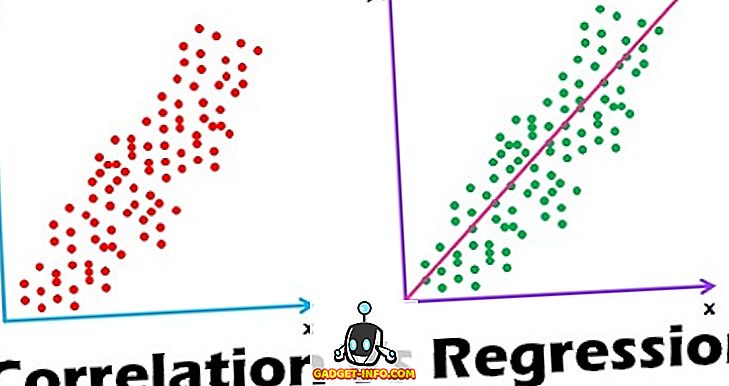
상관 관계 정의
상호라는 용어는 두 단어 'Co'(함께)와 두 개의 양 사이의 관계 (연결)의 두 단어의 조합입니다. 상관 관계는 두 변수를 연구 할 때 한 변수의 단위 변화가 다른 변수 즉, 직접 또는 간접 변수의 동등한 변화에 의해 보복 될 때 관찰됩니다. 그렇지 않으면 한 변수의 이동이 특정 변수의 다른 변수의 이동에 해당하지 않을 때 변수가 상호 연관성이 없다고합니다. 이것은 변수 쌍 사이의 연결 강도를 나타내는 통계 기술입니다.
상관 관계는 양수 또는 음수 일 수 있습니다. 두 변수가 같은 방향으로 움직일 때, 즉 하나의 변수가 증가하면 다른 변수가 증가하고 그 반대 인 경우 변수는 양의 상관 관계가있는 것으로 간주됩니다. 예를 들면 : 이익과 투자.
반대로 두 변수가 다른 방향으로 움직일 때 한 변수의 증가는 다른 변수의 감소를 가져오고 그 반대의 경우도 마찬가지입니다.이 상황을 음의 상관 관계라고합니다. 예 : 제품의 가격 및 수요.
상관 관계의 척도는 다음과 같습니다.
- Karl Pearson의 제품 - 순간 상관 계수
- 스피어 만 순위 상관 계수
- 산포도
- 동시 편차 계수
회귀의 정의
둘 이상의 변수 간의 평균 수학적 관계를 기반으로 한 하나 이상의 독립 변수의 변화로 인한 메트릭 종속 변수의 변화를 추정하기위한 통계 기법을 회귀라고합니다. 그것은 과거 또는 현재의 사건을 기반으로 과거, 현재 또는 미래의 사건을 예측하는 데 사용되는 강력하고 유연한 도구이기 때문에 많은 인간 활동에서 중요한 역할을합니다. 예를 들면 : 과거 기록을 토대로 사업의 미래 이익을 예측할 수 있습니다.
간단한 선형 회귀 분석에서 x와 y의 두 변수가 있습니다. 여기서 y는 x에 의존하거나 x의 영향을받습니다. 여기서 y는 종속 변수 또는 기준 변수로 불리고 x는 독립 변수 또는 예측 변수입니다. x에 대한 y의 회귀선은 다음과 같이 표현됩니다.
y = a + bx
여기서, a = 상수,
b = 회귀 계수,
이 방정식에서 a와 b는 두 회귀 매개 변수입니다.
상관 관계와 회귀의 주요 차이점
아래에 주어진 포인트는 상관 관계와 회귀의 차이를 자세히 설명합니다.
- 두 양의 상호 관계 또는 연관성을 결정하는 통계적 척도를 상관 관계라고합니다. 회귀 분석은 독립 변수가 종속 변수와 어떻게 수치 적으로 관련되는지를 설명합니다.
- 상관 관계는 두 변수 간의 선형 관계를 나타 내기 위해 사용됩니다. 반대로 회귀 분석을 사용하여 최적의 변수를 구하고 변수 하나를 다른 변수를 기반으로 추정합니다.
- 상관 관계에서는 종속 변수와 독립 변수간에 차이가 없습니다. 즉 x와 y 간의 상관 관계는 y와 x와 유사합니다. 반대로, x에 대한 y의 회귀는 y에 대한 x와 다릅니다.
- 상관 관계는 변수 간의 연관성을 나타냅니다. 반대로 회귀 분석은 독립 변수의 단위 변화가 종속 변수에 미치는 영향을 반영합니다.
- 상관 관계는 변수 간의 관계를 나타내는 숫자 값을 찾는 것을 목표로합니다. 고정 변수의 값을 기준으로 임의의 변수의 값을 예측하는 회귀 분석과 달리
결론
위의 논의와 함께이 두 수학 개념은 큰 차이가 있지만, 이 두 이론은 함께 연구되었지만 분명합니다. 상호 관계는 연구자가 연구중인 변수가 상호 연관되어 있는지 여부를 알고 자 할 때 사용되며, 그렇다면 연관성의 강도는 무엇인가? 피어슨의 상관 계수는 상관 관계의 가장 좋은 척도로 간주됩니다. 회귀 분석에서 이벤트에 대한 미래 예측을하기 위해 두 변수 간의 함수 관계가 설정됩니다.